Clustered Multitask GP (w/ Pyro/GPyTorch High-Level Interface)

Introduction

In this example, we use the Pyro integration for a GP model with additional latent variables.

We are modelling a multitask GP in this example. Rather than assuming a linear correlation among the different tasks, we assume that there is cluster structure for the different tasks. Let’s assume there are \(k\) different clusters of tasks. The generative model for task \(i\) is:

\[p(\mathbf y_i \mid \mathbf x_i) = \int \sum_{z_i=1}^k p(\mathbf y_i \mid \mathbf f (\mathbf x_i), z_i) \: p(z_i) \: p(\mathbf f (\mathbf x_i) ) \: d \mathbf f\]

where \(z_i\) is the cluster assignment for task \(i\). There are therefore \(k\) latent functions \(\mathbf f = [f_1 \ldots f_k]\), each modelled by a GP, representing each cluster.

Our goal is therefore to infer:

• The latent functions \(f_1 \ldots f_k\)

• The cluster assignments \(z_i\) for each task

import math
import torch
import pyro
import tqdm
import gpytorch
from matplotlib import pyplot as plt

%matplotlib inline
import matplotlib as mpl
mpl.rc_file_defaults()

# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)

Adding additional latent variables to the likelihood

The standard GPyTorch variational objects will take care of inferring the latent functions \(f_1 \ldots f_k\). However, we do need to add the additional latent variables \(z_i\) to the models. We will do so by creating a custom likelihood that models:

\[\sum_{z_i=1}^k p(\mathbf y_i \mid \mathbf f (\mathbf x_i), z_i) \: p(z_i)\]

GPyTorch’s likelihoods are capable of modeling additional latent variables. Our custom likelihood needs to define the following three functions:

• pyro_model (needs to call through to super().pyro_model at the end), which defines the prior distribution for additional latent variables

• pyro_guide (needs to call through to super().pyro_guide at the end), which defines the variational (guide) distribution for additional latent variables

• forward, which defines the observation distributions conditioned on \mathbf f (\mathbf x_i) and any additional latent variables.

The pyro_model function

For each task, we will model the cluster assignment with a OneHotCategorical variable, where each cluster has equal probability. The pyro_model function will make a pyro.sample call to this prior distribution and then call the super method:

# self.prior_cluster_logits = torch.zeros(num_tasks, num_clusters)

def pyro_model(self, function_dist, target):
    cluster_assignment_samples = pyro.sample(
        self.name_prefix + ".cluster_logits",  # self.name_prefix is added by PyroGP
        pyro.distributions.OneHotCategorical(logits=self.prior_cluster_logits).to_event(1)
    )
    return super().pyro_model(
        function_dist,
        target,
        cluster_assignment_samples=cluster_assignment_samples
    )

Note that we are adding an additional argument cluster_assignment_samples to the super().pyro_model call. This will pass the cluster assignment samples to the forward call, which is necessary for inference.

The pyro_guide function

For each task, the variational (guide) diustribution will also be a OneHotCategorical variable, which will be defined by the parameter self.variational_cluster_logits. The pyro_guide function will make a pyro.sample call to this prior distribution and then call the super method:

def pyro_guide(self, function_dist, target):
    pyro.sample(
        self.name_prefix + ".cluster_logits",  # self.name_prefix is added by PyroGP
        pyro.distributions.OneHotCategorical(logits=self.variational_cluster_logits).to_event(1)
    )
    return super().pyro_guide(function_dist, target)

Note that we are adding an additional argument cluster_assignment_samples to the super().pyro_model call. This will pass the cluster assignment samples to the forward call, which is necessary for inference.

The forward function

The pyro_model fuction passes the additional keyword argument cluster_assignment_samples to the forward call. Therefore, our forward method will define the conditional probability \(p(\mathbf y_i \mid \mathbf f(\mathbf x), z_i)\), where \(\mathbf f(\mathbf x)\) corresponds to the variable function_samples and \(z_i\) corresponds to the variable cluster_assignment_samples.

In our example \(p(\mathbf y_i \mid \mathbf f(\mathbf x), z_i)\) corresponds to a Gaussian noise model.

# self.raw_noise is the Gaussian noise parameter
# function_samples is `n x k`
# cluster_assignment_samples is `k x t`, where `t` is the number of tasks

def forward(self, function_samples, cluster_assignment_samples):
    return pyro.distributions.Normal(
        loc=(function_samples.unsqueeze(-2) * cluster_assignment_samples).sum(-1),
        scale=torch.nn.functional.softplus(self.raw_noise).sqrt()
    ).to_event(1)
    # The to_event call is necessary because we are returning a multitask distribution,
    # where each task dimension corresponds to each of the `t` tasks

This is all we need for inference! However, if we want to use this model to make predictions, the cluster_assignment_samples keyword argument will not be passed into the function. Therefore, we need to make sure that forward can handle both inference and predictions:

def forward(self, function_samples, cluster_assignment_samples=None):
    if cluster_assignment_samples is None:
        # We'll get here at prediction time
        # We'll use the variational distribution when making predictions
        cluster_assignment_samples = pyro.sample(
            self.name_prefix + ".cluster_logits", self._cluster_dist(self.variational_cluster_logits)
        )

    return pyro.distributions.Normal(
        loc=(function_samples.unsqueeze(-2) * cluster_assignment_samples).sum(-1),
        scale=torch.nn.functional.softplus(self.raw_noise).sqrt()
    ).to_event(1)

class ClusterGaussianLikelihood(gpytorch.likelihoods.Likelihood):
    def __init__(self, num_tasks, num_clusters):
        super().__init__()

        # These are parameters/buffers for the cluster assignment latent variables
        self.register_buffer("prior_cluster_logits", torch.zeros(num_tasks, num_clusters))
        self.register_parameter("variational_cluster_logits", torch.nn.Parameter(torch.randn(num_tasks, num_clusters)))

        # The Gaussian observational noise
        self.register_parameter("raw_noise", torch.nn.Parameter(torch.tensor(0.0)))

        # Other info
        self.num_tasks = num_tasks
        self.num_clusters = num_clusters
        self.max_plate_nesting = 1

    def pyro_guide(self, function_dist, target):
        # Here we add the extra variational distribution for the cluster latent variable
        pyro.sample(
            self.name_prefix + ".cluster_logits",  # self.name_prefix is added by PyroGP
            pyro.distributions.OneHotCategorical(logits=self.variational_cluster_logits).to_event(1)
        )
        return super().pyro_guide(function_dist, target)

    def pyro_model(self, function_dist, target):
        # Here we add the extra prior distribution for the cluster latent variable
        cluster_assignment_samples = pyro.sample(
            self.name_prefix + ".cluster_logits",  # self.name_prefix is added by PyroGP
            pyro.distributions.OneHotCategorical(logits=self.prior_cluster_logits).to_event(1)
        )
        return super().pyro_model(function_dist, target, cluster_assignment_samples=cluster_assignment_samples)

    def forward(self, function_samples, cluster_assignment_samples=None):
        # For inference, cluster_assignment_samples will be passed in
        # This bit of code is for when we use the likelihood in the predictive mode
        if cluster_assignment_samples is None:
            cluster_assignment_samples = pyro.sample(
                self.name_prefix + ".cluster_logits",
                pyro.distributions.OneHotCategorical(logits=self.variational_cluster_logits).to_event(1)
            )

        # Now we return the observational distribution, based on the function_samples and cluster_assignment_samples
        res = pyro.distributions.Normal(
            loc=(function_samples.unsqueeze(-2) * cluster_assignment_samples).sum(-1),
            scale=torch.nn.functional.softplus(self.raw_noise).sqrt()
        ).to_event(1)
        return res

Constructing the PyroGP model

The PyroGP model is essentially the same as the model we used in the simple example, except for two changes

• We now will use our more complicated ClusterGaussianLikelihood

• The latent function should be vector valued to correspond to the k latent functions. As a result, we will learn a batched variational distribution, and use a IndependentMultitaskVariationalStrategy to convert the batched variational distribution into a MultitaskMultivariateNormal distribution.

class ClusterMultitaskGPModel(gpytorch.models.pyro.PyroGP):
    def __init__(self, train_x, train_y, num_functions=2, reparam=False):
        num_data = train_y.size(-2)

        # Define all the variational stuff
        inducing_points = torch.linspace(0, 1, 64).unsqueeze(-1)
        variational_distribution = gpytorch.variational.CholeskyVariationalDistribution(
            num_inducing_points=inducing_points.size(-2),
            batch_shape=torch.Size([num_functions])
        )

        # Here we're using a IndependentMultitaskVariationalStrategy - so that the output of the
        # GP latent function is a MultitaskMultivariateNormal
        variational_strategy = gpytorch.variational.IndependentMultitaskVariationalStrategy(
            gpytorch.variational.VariationalStrategy(self, inducing_points, variational_distribution),
            num_tasks=num_functions,
        )

        # Standard initializtation
        likelihood = ClusterGaussianLikelihood(train_y.size(-1), num_functions)
        super().__init__(variational_strategy, likelihood, num_data=num_data)
        self.likelihood = likelihood
        self.num_functions = num_functions

        # Mean, covar
        self.mean_module = gpytorch.means.ZeroMean()
        self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        res = gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
        return res

This model can now be used to perform inference on cluster assignments, as well as make predictions using the inferred cluster assignments!

train_x = torch.linspace(0, 1, 100)
train_y = torch.stack([
    torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2,
    torch.cos(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2,
    torch.sin(train_x * (2 * math.pi)) + 2 * torch.cos(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2,
    -torch.cos(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2,
], -1)
num_tasks = train_y.size(-1)

pyro.clear_param_store()
model = ClusterMultitaskGPModel(train_x, train_y, num_functions=2)
num_particles = 1 if smoke_test else 64
num_iter = 4 if smoke_test else 1000

def train(lr=0.01):
    optimizer = pyro.optim.Adam({"lr": 0.1})
    elbo = pyro.infer.Trace_ELBO(num_particles=num_particles, vectorize_particles=True, retain_graph=True)
    svi = pyro.infer.SVI(model.model, model.guide, optimizer, elbo)
    model.train()

    iterator = tqdm.notebook.tqdm(range(num_iter))
    for i in iterator:
        model.zero_grad()
        loss = svi.step(train_x, train_y)
        iterator.set_postfix(loss=loss)

%time train()

CPU times: user 1min 29s, sys: 2.59 s, total: 1min 32s
Wall time: 15.4 s

# Set into eval mode and make predictions
model.eval()
with torch.no_grad():
    test_x = torch.linspace(0, 1, 51)
    predictions = model.likelihood(model(test_x)).rsample()
print(predictions.shape)  # num_samples x num_data x num_tasks

fig, axs = plt.subplots(1, num_tasks, figsize=(4 * num_tasks, 3))
for task, ax in enumerate(axs):
    ax.plot(train_x.detach().numpy(), train_y[:, task].detach().numpy(), 'k*')
    ax.plot(test_x.numpy(), predictions[:, :, task].T.numpy(), 'b', lw=1, alpha=0.2)
    ax.set_ylim([-3, 3])
    ax.legend(['Observed Data', 'Mean', 'Confidence'])
    ax.set_title(f'Task {task + 1}')

fig.tight_layout()
None

torch.Size([10, 51, 4])

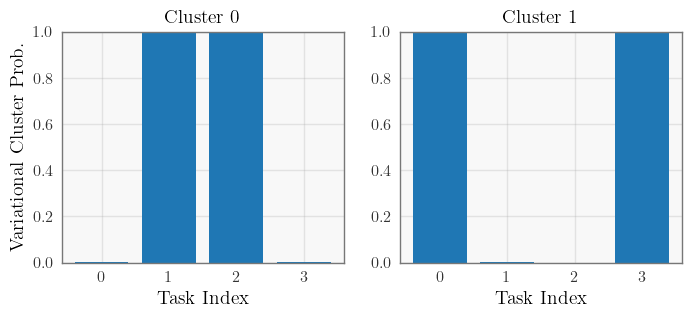
# Infer cluster assignments
variational_clusters = pyro.distributions.Categorical(logits=model.likelihood.variational_cluster_logits).probs

# Plot cluster assignments
fig, axs = plt.subplots(1, model.num_functions, figsize=(4 * model.num_functions, 3))
for function, ax in enumerate(axs):
    index = torch.arange(num_tasks)
    ax.bar(index, variational_clusters[:, function].detach().numpy())
    ax.set(ylim=[0, 1], title=f"Cluster {function}", xlabel="Task Index")
axs[0].set_ylabel("Variational Cluster Prob.")
None