GP Regression with Grid Structured Training Data¶
In this notebook, we demonstrate how to perform GP regression when your training data lies on a regularly spaced grid. For this example, we’ll be modeling a 2D function where the training data is on an evenly spaced grid on (0,1)x(0, 2) with 100 grid points in each dimension.
In other words, we have 10000 training examples. However, the grid structure of the training data will allow us to perform inference very quickly anyways.
[1]:
import gpytorch
import torch
import math
Make the grid and training data¶
In the next cell, we create the grid, along with the 10000 training examples and labels. After running this cell, we create three important tensors:
gridis a tensor that isgrid_size x 2and contains the 1D grid for each dimension.train_xis a tensor containing the full 10000 training examples.train_yare the labels. For this, we’re just using a simple sine function.
[2]:
grid_bounds = [(0, 1), (0, 2)]
grid_size = 25
grid = torch.zeros(grid_size, len(grid_bounds))
for i in range(len(grid_bounds)):
grid_diff = float(grid_bounds[i][1] - grid_bounds[i][0]) / (grid_size - 2)
grid[:, i] = torch.linspace(grid_bounds[i][0] - grid_diff, grid_bounds[i][1] + grid_diff, grid_size)
train_x = gpytorch.utils.grid.create_data_from_grid(grid)
train_y = torch.sin((train_x[:, 0] + train_x[:, 1]) * (2 * math.pi)) + torch.randn_like(train_x[:, 0]).mul(0.01)
Creating the Grid GP Model¶
In the next cell we create our GP model. Like other scalable GP methods, we’ll use a scalable kernel that wraps a base kernel. In this case, we create a GridKernel that wraps an RBFKernel.
[3]:
class GridGPRegressionModel(gpytorch.models.ExactGP):
def __init__(self, grid, train_x, train_y, likelihood):
super(GridGPRegressionModel, self).__init__(train_x, train_y, likelihood)
num_dims = train_x.size(-1)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.GridKernel(gpytorch.kernels.RBFKernel(), grid=grid)
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = GridGPRegressionModel(grid, train_x, train_y, likelihood)
[4]:
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iter = 2 if smoke_test else 50
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.1) # Includes GaussianLikelihood parameters
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
for i in range(training_iter):
# Zero gradients from previous iteration
optimizer.zero_grad()
# Output from model
output = model(train_x)
# Calc loss and backprop gradients
loss = -mll(output, train_y)
loss.backward()
print('Iter %d/%d - Loss: %.3f lengthscale: %.3f noise: %.3f' % (
i + 1, training_iter, loss.item(),
model.covar_module.base_kernel.lengthscale.item(),
model.likelihood.noise.item()
))
optimizer.step()
Iter 1/50 - Loss: 0.978 lengthscale: 0.693 noise: 0.693
Iter 2/50 - Loss: 0.933 lengthscale: 0.644 noise: 0.644
Iter 3/50 - Loss: 0.880 lengthscale: 0.598 noise: 0.598
Iter 4/50 - Loss: 0.816 lengthscale: 0.554 noise: 0.554
Iter 5/50 - Loss: 0.738 lengthscale: 0.513 noise: 0.513
Iter 6/50 - Loss: 0.655 lengthscale: 0.474 noise: 0.473
Iter 7/50 - Loss: 0.575 lengthscale: 0.438 noise: 0.436
Iter 8/50 - Loss: 0.507 lengthscale: 0.403 noise: 0.401
Iter 9/50 - Loss: 0.450 lengthscale: 0.372 noise: 0.368
Iter 10/50 - Loss: 0.398 lengthscale: 0.345 noise: 0.338
Iter 11/50 - Loss: 0.351 lengthscale: 0.321 noise: 0.309
Iter 12/50 - Loss: 0.306 lengthscale: 0.301 noise: 0.282
Iter 13/50 - Loss: 0.259 lengthscale: 0.283 noise: 0.258
Iter 14/50 - Loss: 0.214 lengthscale: 0.269 noise: 0.235
Iter 15/50 - Loss: 0.167 lengthscale: 0.256 noise: 0.213
Iter 16/50 - Loss: 0.120 lengthscale: 0.245 noise: 0.194
Iter 17/50 - Loss: 0.075 lengthscale: 0.236 noise: 0.176
Iter 18/50 - Loss: 0.027 lengthscale: 0.228 noise: 0.160
Iter 19/50 - Loss: -0.021 lengthscale: 0.222 noise: 0.145
Iter 20/50 - Loss: -0.067 lengthscale: 0.217 noise: 0.131
Iter 21/50 - Loss: -0.118 lengthscale: 0.213 noise: 0.118
Iter 22/50 - Loss: -0.167 lengthscale: 0.210 noise: 0.107
Iter 23/50 - Loss: -0.213 lengthscale: 0.208 noise: 0.097
Iter 24/50 - Loss: -0.267 lengthscale: 0.207 noise: 0.087
Iter 25/50 - Loss: -0.311 lengthscale: 0.207 noise: 0.079
Iter 26/50 - Loss: -0.363 lengthscale: 0.208 noise: 0.071
Iter 27/50 - Loss: -0.414 lengthscale: 0.209 noise: 0.064
Iter 28/50 - Loss: -0.460 lengthscale: 0.212 noise: 0.057
Iter 29/50 - Loss: -0.514 lengthscale: 0.216 noise: 0.052
Iter 30/50 - Loss: -0.563 lengthscale: 0.221 noise: 0.047
Iter 31/50 - Loss: -0.616 lengthscale: 0.227 noise: 0.042
Iter 32/50 - Loss: -0.668 lengthscale: 0.234 noise: 0.038
Iter 33/50 - Loss: -0.717 lengthscale: 0.243 noise: 0.034
Iter 34/50 - Loss: -0.773 lengthscale: 0.253 noise: 0.031
Iter 35/50 - Loss: -0.821 lengthscale: 0.264 noise: 0.027
Iter 36/50 - Loss: -0.868 lengthscale: 0.276 noise: 0.025
Iter 37/50 - Loss: -0.927 lengthscale: 0.290 noise: 0.022
Iter 38/50 - Loss: -0.981 lengthscale: 0.305 noise: 0.020
Iter 39/50 - Loss: -1.026 lengthscale: 0.320 noise: 0.018
Iter 40/50 - Loss: -1.084 lengthscale: 0.338 noise: 0.016
Iter 41/50 - Loss: -1.133 lengthscale: 0.355 noise: 0.014
Iter 42/50 - Loss: -1.183 lengthscale: 0.371 noise: 0.013
Iter 43/50 - Loss: -1.231 lengthscale: 0.385 noise: 0.012
Iter 44/50 - Loss: -1.277 lengthscale: 0.397 noise: 0.011
Iter 45/50 - Loss: -1.323 lengthscale: 0.402 noise: 0.009
Iter 46/50 - Loss: -1.374 lengthscale: 0.403 noise: 0.008
Iter 47/50 - Loss: -1.426 lengthscale: 0.401 noise: 0.008
Iter 48/50 - Loss: -1.481 lengthscale: 0.395 noise: 0.007
Iter 49/50 - Loss: -1.529 lengthscale: 0.388 noise: 0.006
Iter 50/50 - Loss: -1.576 lengthscale: 0.379 noise: 0.006
In the next cell, we create a set of 400 test examples and make predictions. Note that unlike other scalable GP methods, testing is more complicated. Because our test data can be different from the training data, in general we may not be able to avoid creating a num_train x num_test (e.g., 10000 x 400) kernel matrix between the training and test data.
For this reason, if you have large numbers of test points, memory may become a concern. The time complexity should still be reasonable, however, because we will still exploit structure in the train-train covariance matrix.
[5]:
model.eval()
likelihood.eval()
n = 20
test_x = torch.zeros(int(pow(n, 2)), 2)
for i in range(n):
for j in range(n):
test_x[i * n + j][0] = float(i) / (n-1)
test_x[i * n + j][1] = float(j) / (n-1)
with torch.no_grad(), gpytorch.settings.fast_pred_var():
observed_pred = likelihood(model(test_x))
[6]:
import matplotlib.pyplot as plt
%matplotlib inline
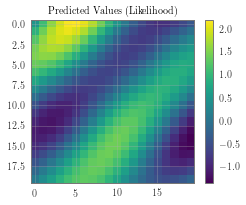
pred_labels = observed_pred.mean.view(n, n)
# Calc abosolute error
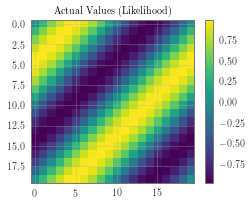
test_y_actual = torch.sin(((test_x[:, 0] + test_x[:, 1]) * (2 * math.pi))).view(n, n)
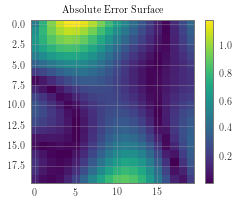
delta_y = torch.abs(pred_labels - test_y_actual).detach().numpy()
# Define a plotting function
def ax_plot(f, ax, y_labels, title):
if smoke_test: return # this is for running the notebook in our testing framework
im = ax.imshow(y_labels)
ax.set_title(title)
f.colorbar(im)
# Plot our predictive means
f, observed_ax = plt.subplots(1, 1, figsize=(4, 3))
ax_plot(f, observed_ax, pred_labels, 'Predicted Values (Likelihood)')
# Plot the true values
f, observed_ax2 = plt.subplots(1, 1, figsize=(4, 3))
ax_plot(f, observed_ax2, test_y_actual, 'Actual Values (Likelihood)')
# Plot the absolute errors
f, observed_ax3 = plt.subplots(1, 1, figsize=(4, 3))
ax_plot(f, observed_ax3, delta_y, 'Absolute Error Surface')
[ ]: