Implementing a custom kernel in GPyTorch

In this notebook we are looking at how to implement a custom kernel in GPyTorch. As an example, we consider the sinc kernel.

import math
import torch
import gpytorch
from matplotlib import pyplot as plt

Before we start, let’s set up some training data and convenience functions

import os
smoke_test = ('CI' in os.environ)
training_iter = 2 if smoke_test else 50

# Training data is 100 points in [0,1] inclusive regularly spaced
train_x = torch.linspace(0, 1, 100)
# True function is sin(2*pi*x) with Gaussian noise
train_y = torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * math.sqrt(0.04)

# Wrap training, prediction and plotting from the ExactGP-Tutorial into a function,
# so that we do not have to repeat the code later on
def train(model, likelihood, training_iter=training_iter):
    # Use the adam optimizer
    optimizer = torch.optim.Adam(model.parameters(), lr=0.1)  # Includes GaussianLikelihood parameters

    # "Loss" for GPs - the marginal log likelihood
    mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)

    for i in range(training_iter):
        # Zero gradients from previous iteration
        optimizer.zero_grad()
        # Output from model
        output = model(train_x)
        # Calc loss and backprop gradients
        loss = -mll(output, train_y)
        loss.backward()
        optimizer.step()


def predict(model, likelihood, test_x = torch.linspace(0, 1, 51)):
    model.eval()
    likelihood.eval()
    # Make predictions by feeding model through likelihood
    with torch.no_grad(), gpytorch.settings.fast_pred_var():
        # Test points are regularly spaced along [0,1]
        return likelihood(model(test_x))

def plot(observed_pred, test_x=torch.linspace(0, 1, 51)):
    with torch.no_grad():
        # Initialize plot
        f, ax = plt.subplots(1, 1, figsize=(4, 3))

        # Get upper and lower confidence bounds
        lower, upper = observed_pred.confidence_region()
        # Plot training data as black stars
        ax.plot(train_x.numpy(), train_y.numpy(), 'k*')
        # Plot predictive means as blue line
        ax.plot(test_x.numpy(), observed_pred.mean.numpy(), 'b')
        # Shade between the lower and upper confidence bounds
        ax.fill_between(test_x.numpy(), lower.numpy(), upper.numpy(), alpha=0.5)
        ax.set_ylim([-3, 3])
        ax.legend(['Observed Data', 'Mean', 'Confidence'])

A first kernel

To implement a custom kernel, we derive one from GPyTorch’s kernel class and implement the forward() method. The base class provides many useful routines. For example, __call__() is implemented, so that the kernel may be called directly, without resorting to the forward() routine. Among other things, the Kernel class provides a method covar_dist(), which may be used to calculate the Euclidian distance between point pairs conveniently.

The forward() method represents the kernel function and should return a torch.tensor or a linear_operator.operators.LinearOperator, when called on two torch.tensors:

class FirstSincKernel(gpytorch.kernels.Kernel):
    # the sinc kernel is stationary
    is_stationary = True

    # this is the kernel function
    def forward(self, x1, x2, **params):
        # calculate the distance between inputs
        diff = self.covar_dist(x1, x2, **params)
        # prevent divide by 0 errors
        diff.where(diff == 0, torch.as_tensor(1e-20))
        # return sinc(diff) = sin(diff) / diff
        return torch.sin(diff).div(diff)

We can now already use this kernel. We therefore define a GP-model, similar to the tutorial on exact GP inference:

# Use the simplest form of GP model, exact inference
class FirstGPModel(gpytorch.models.ExactGP):
    def __init__(self, train_x, train_y, likelihood):
        super().__init__(train_x, train_y, likelihood)
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = FirstSincKernel()

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

By using the convenience routines from above, the model can be trained and evaluated:

# initialize likelihood and model
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = FirstGPModel(train_x, train_y, likelihood)

# set to training mode and train
model.train()
likelihood.train()
train(model, likelihood)

# Get into evaluation (predictive posterior) mode and predict
model.eval()
likelihood.eval()
observed_pred = predict(model, likelihood)
# plot results
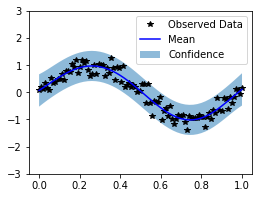
plot(observed_pred)

/home/arthus/miniconda3/envs/torch-toying/lib/python3.8/site-packages/torch/autograd/__init__.py:130: UserWarning: CUDA initialization: Found no NVIDIA driver on your system. Please check that you have an NVIDIA GPU and installed a driver from http://www.nvidia.com/Download/index.aspx (Triggered internally at  /opt/conda/conda-bld/pytorch_1603729096996/work/c10/cuda/CUDAFunctions.cpp:100.)
  Variable._execution_engine.run_backward(

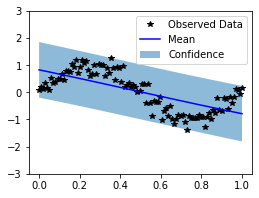
Clearly, the kernel doesn’t perform well. This is due to the lack of a lengthscale parameter, which we will add next.

Adding hyperparameters

Although the FirstSincKernel can be used for defining a model, it lacks a parameter that controls the correlation length. This lengthscale will be implemented as a hyperparameter. See also the tutorial on hyperparamaters, for information on raw vs. actual parameters.

The parameter has to be registered, using the method register_parameter(), which Kernel inherits from Module. Similarly, we register constraints and priors.

# import positivity constraint
from gpytorch.constraints import Positive

class SincKernel(gpytorch.kernels.Kernel):
    # the sinc kernel is stationary
    is_stationary = True

    # We will register the parameter when initializing the kernel
    def __init__(self, length_prior=None, length_constraint=None, **kwargs):
        super().__init__(**kwargs)

        # register the raw parameter
        self.register_parameter(
            name='raw_length', parameter=torch.nn.Parameter(torch.zeros(*self.batch_shape, 1, 1))
        )

        # set the parameter constraint to be positive, when nothing is specified
        if length_constraint is None:
            length_constraint = Positive()

        # register the constraint
        self.register_constraint("raw_length", length_constraint)

        # set the parameter prior, see
        # https://docs.gpytorch.ai/en/latest/module.html#gpytorch.Module.register_prior
        if length_prior is not None:
            self.register_prior(
                "length_prior",
                length_prior,
                lambda m: m.length,
                lambda m, v : m._set_length(v),
            )

    # now set up the 'actual' paramter
    @property
    def length(self):
        # when accessing the parameter, apply the constraint transform
        return self.raw_length_constraint.transform(self.raw_length)

    @length.setter
    def length(self, value):
        return self._set_length(value)

    def _set_length(self, value):
        if not torch.is_tensor(value):
            value = torch.as_tensor(value).to(self.raw_length)
        # when setting the paramater, transform the actual value to a raw one by applying the inverse transform
        self.initialize(raw_length=self.raw_length_constraint.inverse_transform(value))

    # this is the kernel function
    def forward(self, x1, x2, **params):
        # apply lengthscale
        x1_ = x1.div(self.length)
        x2_ = x2.div(self.length)
        # calculate the distance between inputs
        diff = self.covar_dist(x1_, x2_, **params)
        # prevent divide by 0 errors
        diff.where(diff == 0, torch.as_tensor(1e-20))
        # return sinc(diff) = sin(diff) / diff
        return torch.sin(diff).div(diff)

We can now define a new GPModel, train it and make predictions:

# Use the simplest form of GP model, exact inference
class SincGPModel(gpytorch.models.ExactGP):
    def __init__(self, train_x, train_y, likelihood):
        super().__init__(train_x, train_y, likelihood)
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = SincKernel()

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

# initialize the new model
model = SincGPModel(train_x, train_y, likelihood)

# set to training mode and train
model.train()
likelihood.train()
train(model, likelihood)

# Get into evaluation (predictive posterior) mode and predict
model.eval()
likelihood.eval()
observed_pred = predict(model, likelihood)
# plot results
plot(observed_pred)

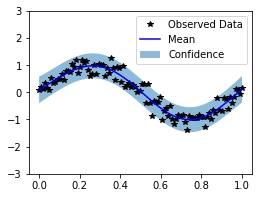
Because many kernels use a lengthscale, there is actually a simpler way to implement it, by using the has_lengthscale attribute from Kernel.

class SimpleSincKernel(gpytorch.kernels.Kernel):
    has_lengthscale = True

    # this is the kernel function
    def forward(self, x1, x2, **params):
        # apply lengthscale
        x1_ = x1.div(self.lengthscale)
        x2_ = x2.div(self.lengthscale)
        # calculate the distance between inputs
        diff = self.covar_dist(x1_, x2_, **params)
        # prevent divide by 0 errors
        diff.where(diff == 0, torch.as_tensor(1e-20))
        # return sinc(diff) = sin(diff) / diff
        return torch.sin(diff).div(diff)

# Use the simplest form of GP model, exact inference
class SimpleSincGPModel(gpytorch.models.ExactGP):
    def __init__(self, train_x, train_y, likelihood):
        super().__init__(train_x, train_y, likelihood)
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = SimpleSincKernel()

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

# initialize the new model
model = SimpleSincGPModel(train_x, train_y, likelihood)

# set to training mode and train
model.train()
likelihood.train()
train(model, likelihood)

# Get into evaluation (predictive posterior) mode and predict
model.eval()
likelihood.eval()
observed_pred = predict(model, likelihood)
# plot results
plot(observed_pred)