Multitask GP Regression¶
Introduction¶
Multitask regression, introduced in this paper learns similarities in the outputs simultaneously. It’s useful when you are performing regression on multiple functions that share the same inputs, especially if they have similarities (such as being sinusodial).
Given inputs \(x\) and \(x'\), and tasks \(i\) and \(j\), the covariance between two datapoints and two tasks is given by
where \(k_\text{inputs}\) is a standard kernel (e.g. RBF) that operates on the inputs. \(k_\text{task}\) is a lookup table containing inter-task covariance.
[1]:
import math
import torch
import gpytorch
from matplotlib import pyplot as plt
%matplotlib inline
%load_ext autoreload
%autoreload 2
Set up training data¶
In the next cell, we set up the training data for this example. We’ll be using 100 regularly spaced points on [0,1] which we evaluate the function on and add Gaussian noise to get the training labels.
We’ll have two functions - a sine function (y1) and a cosine function (y2).
For MTGPs, our train_targets will actually have two dimensions: with the second dimension corresponding to the different tasks.
[2]:
train_x = torch.linspace(0, 1, 100)
train_y = torch.stack([
torch.sin(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2,
torch.cos(train_x * (2 * math.pi)) + torch.randn(train_x.size()) * 0.2,
], -1)
Define a multitask model¶
The model should be somewhat similar to the ExactGP model in the simple regression example. The differences:
We’re going to wrap ConstantMean with a
MultitaskMean. This makes sure we have a mean function for each task.Rather than just using a RBFKernel, we’re using that in conjunction with a
MultitaskKernel. This gives us the covariance function described in the introduction.We’re using a
MultitaskMultivariateNormalandMultitaskGaussianLikelihood. This allows us to deal with the predictions/outputs in a nice way. For example, when we call MultitaskMultivariateNormal.mean, we get an x num_tasksmatrix back.
You may also notice that we don’t use a ScaleKernel, since the MultitaskKernel will do some scaling for us. (This way we’re not overparameterizing the kernel.)
[3]:
class MultitaskGPModel(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super(MultitaskGPModel, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.MultitaskMean(
gpytorch.means.ConstantMean(), num_tasks=2
)
self.covar_module = gpytorch.kernels.MultitaskKernel(
gpytorch.kernels.RBFKernel(), num_tasks=2, rank=1
)
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultitaskMultivariateNormal(mean_x, covar_x)
likelihood = gpytorch.likelihoods.MultitaskGaussianLikelihood(num_tasks=2)
model = MultitaskGPModel(train_x, train_y, likelihood)
Train the model hyperparameters¶
[4]:
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iterations = 2 if smoke_test else 50
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.1) # Includes GaussianLikelihood parameters
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
for i in range(training_iterations):
optimizer.zero_grad()
output = model(train_x)
loss = -mll(output, train_y)
loss.backward()
print('Iter %d/%d - Loss: %.3f' % (i + 1, training_iterations, loss.item()))
optimizer.step()
Iter 1/50 - Loss: 1.220
Iter 2/50 - Loss: 1.180
Iter 3/50 - Loss: 1.138
Iter 4/50 - Loss: 1.096
Iter 5/50 - Loss: 1.054
Iter 6/50 - Loss: 1.013
Iter 7/50 - Loss: 0.972
Iter 8/50 - Loss: 0.932
Iter 9/50 - Loss: 0.892
Iter 10/50 - Loss: 0.854
Iter 11/50 - Loss: 0.815
Iter 12/50 - Loss: 0.777
Iter 13/50 - Loss: 0.739
Iter 14/50 - Loss: 0.700
Iter 15/50 - Loss: 0.660
Iter 16/50 - Loss: 0.620
Iter 17/50 - Loss: 0.579
Iter 18/50 - Loss: 0.538
Iter 19/50 - Loss: 0.497
Iter 20/50 - Loss: 0.456
Iter 21/50 - Loss: 0.415
Iter 22/50 - Loss: 0.376
Iter 23/50 - Loss: 0.338
Iter 24/50 - Loss: 0.301
Iter 25/50 - Loss: 0.265
Iter 26/50 - Loss: 0.231
Iter 27/50 - Loss: 0.197
Iter 28/50 - Loss: 0.165
Iter 29/50 - Loss: 0.134
Iter 30/50 - Loss: 0.104
Iter 31/50 - Loss: 0.076
Iter 32/50 - Loss: 0.050
Iter 33/50 - Loss: 0.027
Iter 34/50 - Loss: 0.006
Iter 35/50 - Loss: -0.012
Iter 36/50 - Loss: -0.027
Iter 37/50 - Loss: -0.040
Iter 38/50 - Loss: -0.051
Iter 39/50 - Loss: -0.059
Iter 40/50 - Loss: -0.065
Iter 41/50 - Loss: -0.068
Iter 42/50 - Loss: -0.070
Iter 43/50 - Loss: -0.069
Iter 44/50 - Loss: -0.068
Iter 45/50 - Loss: -0.066
Iter 46/50 - Loss: -0.063
Iter 47/50 - Loss: -0.060
Iter 48/50 - Loss: -0.057
Iter 49/50 - Loss: -0.055
Iter 50/50 - Loss: -0.053
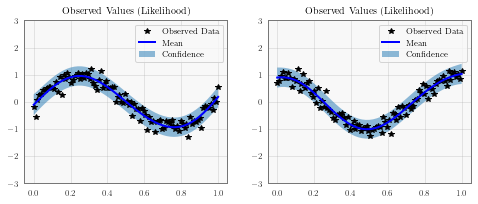
Make predictions with the model¶
[5]:
# Set into eval mode
model.eval()
likelihood.eval()
# Initialize plots
f, (y1_ax, y2_ax) = plt.subplots(1, 2, figsize=(8, 3))
# Make predictions
with torch.no_grad(), gpytorch.settings.fast_pred_var():
test_x = torch.linspace(0, 1, 51)
predictions = likelihood(model(test_x))
mean = predictions.mean
lower, upper = predictions.confidence_region()
# This contains predictions for both tasks, flattened out
# The first half of the predictions is for the first task
# The second half is for the second task
# Plot training data as black stars
y1_ax.plot(train_x.detach().numpy(), train_y[:, 0].detach().numpy(), 'k*')
# Predictive mean as blue line
y1_ax.plot(test_x.numpy(), mean[:, 0].numpy(), 'b')
# Shade in confidence
y1_ax.fill_between(test_x.numpy(), lower[:, 0].numpy(), upper[:, 0].numpy(), alpha=0.5)
y1_ax.set_ylim([-3, 3])
y1_ax.legend(['Observed Data', 'Mean', 'Confidence'])
y1_ax.set_title('Observed Values (Likelihood)')
# Plot training data as black stars
y2_ax.plot(train_x.detach().numpy(), train_y[:, 1].detach().numpy(), 'k*')
# Predictive mean as blue line
y2_ax.plot(test_x.numpy(), mean[:, 1].numpy(), 'b')
# Shade in confidence
y2_ax.fill_between(test_x.numpy(), lower[:, 1].numpy(), upper[:, 1].numpy(), alpha=0.5)
y2_ax.set_ylim([-3, 3])
y2_ax.legend(['Observed Data', 'Mean', 'Confidence'])
y2_ax.set_title('Observed Values (Likelihood)')
None
[ ]: