GPyTorch regression with derivative information in 2d¶
Introduction¶
In this notebook, we show how to train a GP regression model in GPyTorch of a 2-dimensional function given function values and derivative observations. We consider modeling the Franke function where the values and derivatives are contaminated with independent \(\mathcal{N}(0, 0.5)\) distributed noise.
[1]:
import torch
import gpytorch
import math
from matplotlib import cm
from matplotlib import pyplot as plt
import numpy as np
%matplotlib inline
%load_ext autoreload
%autoreload 2
Franke function¶
The following is a vectorized implementation of the 2-dimensional Franke function (https://www.sfu.ca/~ssurjano/franke2d.html)
[2]:
def franke(X, Y):
term1 = .75*torch.exp(-((9*X - 2).pow(2) + (9*Y - 2).pow(2))/4)
term2 = .75*torch.exp(-((9*X + 1).pow(2))/49 - (9*Y + 1)/10)
term3 = .5*torch.exp(-((9*X - 7).pow(2) + (9*Y - 3).pow(2))/4)
term4 = .2*torch.exp(-(9*X - 4).pow(2) - (9*Y - 7).pow(2))
f = term1 + term2 + term3 - term4
dfx = -2*(9*X - 2)*9/4 * term1 - 2*(9*X + 1)*9/49 * term2 + \
-2*(9*X - 7)*9/4 * term3 + 2*(9*X - 4)*9 * term4
dfy = -2*(9*Y - 2)*9/4 * term1 - 9/10 * term2 + \
-2*(9*Y - 3)*9/4 * term3 + 2*(9*Y - 7)*9 * term4
return f, dfx, dfy
Setting up the training data¶
We use a grid with 100 points in \([0,1] \times [0,1]\) with 10 uniformly distributed points per dimension.
[3]:
xv, yv = torch.meshgrid([torch.linspace(0, 1, 10), torch.linspace(0, 1, 10)])
train_x = torch.cat((
xv.contiguous().view(xv.numel(), 1),
yv.contiguous().view(yv.numel(), 1)),
dim=1
)
f, dfx, dfy = franke(train_x[:, 0], train_x[:, 1])
train_y = torch.stack([f, dfx, dfy], -1).squeeze(1)
train_y += 0.05 * torch.randn(train_y.size()) # Add noise to both values and gradients
Setting up the model¶
A GP prior on the function values implies a multi-output GP prior on the function values and the partial derivatives, see 9.4 in http://www.gaussianprocess.org/gpml/chapters/RW9.pdf for more details. This allows using a MultitaskMultivariateNormal and MultitaskGaussianLikelihood to train a GP model from both function values and gradients. The resulting RBF kernel that models the covariance between the values and partial derivatives has been implemented in RBFKernelGrad and the
extension of a constant mean is implemented in ConstantMeanGrad.
[4]:
class GPModelWithDerivatives(gpytorch.models.ExactGP):
def __init__(self, train_x, train_y, likelihood):
super(GPModelWithDerivatives, self).__init__(train_x, train_y, likelihood)
self.mean_module = gpytorch.means.ConstantMeanGrad()
self.base_kernel = gpytorch.kernels.RBFKernelGrad(ard_num_dims=2)
self.covar_module = gpytorch.kernels.ScaleKernel(self.base_kernel)
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultitaskMultivariateNormal(mean_x, covar_x)
likelihood = gpytorch.likelihoods.MultitaskGaussianLikelihood(num_tasks=3) # Value + x-derivative + y-derivative
model = GPModelWithDerivatives(train_x, train_y, likelihood)
The model training is similar to training a standard GP regression model
[5]:
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iter = 2 if smoke_test else 50
# Find optimal model hyperparameters
model.train()
likelihood.train()
# Use the adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=0.05) # Includes GaussianLikelihood parameters
# "Loss" for GPs - the marginal log likelihood
mll = gpytorch.mlls.ExactMarginalLogLikelihood(likelihood, model)
for i in range(training_iter):
optimizer.zero_grad()
output = model(train_x)
loss = -mll(output, train_y)
loss.backward()
print("Iter %d/%d - Loss: %.3f lengthscales: %.3f, %.3f noise: %.3f" % (
i + 1, training_iter, loss.item(),
model.covar_module.base_kernel.lengthscale.squeeze()[0],
model.covar_module.base_kernel.lengthscale.squeeze()[1],
model.likelihood.noise.item()
))
optimizer.step()
Iter 1/100 - Loss: 128.629 lengthscales: 0.693, 0.693 noise: 0.693
Iter 2/100 - Loss: 127.182 lengthscales: 0.668, 0.668 noise: 0.668
Iter 3/100 - Loss: 125.838 lengthscales: 0.644, 0.645 noise: 0.644
Iter 4/100 - Loss: 123.982 lengthscales: 0.624, 0.621 noise: 0.621
Iter 5/100 - Loss: 122.799 lengthscales: 0.604, 0.598 noise: 0.598
Iter 6/100 - Loss: 120.909 lengthscales: 0.583, 0.576 noise: 0.576
Iter 7/100 - Loss: 119.255 lengthscales: 0.562, 0.555 noise: 0.554
Iter 8/100 - Loss: 117.506 lengthscales: 0.542, 0.534 noise: 0.533
Iter 9/100 - Loss: 116.083 lengthscales: 0.522, 0.513 noise: 0.513
Iter 10/100 - Loss: 113.978 lengthscales: 0.502, 0.493 noise: 0.493
Iter 11/100 - Loss: 112.242 lengthscales: 0.482, 0.474 noise: 0.473
Iter 12/100 - Loss: 110.389 lengthscales: 0.463, 0.455 noise: 0.455
Iter 13/100 - Loss: 108.644 lengthscales: 0.444, 0.436 noise: 0.436
Iter 14/100 - Loss: 107.660 lengthscales: 0.426, 0.418 noise: 0.419
Iter 15/100 - Loss: 104.480 lengthscales: 0.408, 0.402 noise: 0.401
Iter 16/100 - Loss: 103.058 lengthscales: 0.391, 0.387 noise: 0.385
Iter 17/100 - Loss: 101.174 lengthscales: 0.374, 0.373 noise: 0.369
Iter 18/100 - Loss: 98.379 lengthscales: 0.358, 0.361 noise: 0.353
Iter 19/100 - Loss: 96.482 lengthscales: 0.343, 0.352 noise: 0.338
Iter 20/100 - Loss: 95.282 lengthscales: 0.327, 0.344 noise: 0.323
Iter 21/100 - Loss: 92.911 lengthscales: 0.313, 0.339 noise: 0.309
Iter 22/100 - Loss: 89.532 lengthscales: 0.300, 0.335 noise: 0.295
Iter 23/100 - Loss: 89.324 lengthscales: 0.288, 0.332 noise: 0.282
Iter 24/100 - Loss: 86.490 lengthscales: 0.279, 0.329 noise: 0.269
Iter 25/100 - Loss: 85.546 lengthscales: 0.272, 0.328 noise: 0.257
Iter 26/100 - Loss: 83.578 lengthscales: 0.268, 0.327 noise: 0.245
Iter 27/100 - Loss: 81.732 lengthscales: 0.265, 0.326 noise: 0.234
Iter 28/100 - Loss: 79.472 lengthscales: 0.265, 0.326 noise: 0.223
Iter 29/100 - Loss: 77.669 lengthscales: 0.267, 0.327 noise: 0.212
Iter 30/100 - Loss: 75.215 lengthscales: 0.269, 0.329 noise: 0.202
Iter 31/100 - Loss: 73.676 lengthscales: 0.272, 0.329 noise: 0.193
Iter 32/100 - Loss: 70.514 lengthscales: 0.276, 0.328 noise: 0.183
Iter 33/100 - Loss: 69.765 lengthscales: 0.280, 0.325 noise: 0.175
Iter 34/100 - Loss: 68.525 lengthscales: 0.284, 0.320 noise: 0.166
Iter 35/100 - Loss: 66.181 lengthscales: 0.287, 0.314 noise: 0.158
Iter 36/100 - Loss: 62.446 lengthscales: 0.288, 0.307 noise: 0.150
Iter 37/100 - Loss: 62.009 lengthscales: 0.287, 0.299 noise: 0.143
Iter 38/100 - Loss: 58.204 lengthscales: 0.284, 0.290 noise: 0.136
Iter 39/100 - Loss: 57.167 lengthscales: 0.280, 0.281 noise: 0.130
Iter 40/100 - Loss: 54.072 lengthscales: 0.274, 0.271 noise: 0.123
Iter 41/100 - Loss: 51.696 lengthscales: 0.268, 0.261 noise: 0.117
Iter 42/100 - Loss: 49.792 lengthscales: 0.261, 0.253 noise: 0.111
Iter 43/100 - Loss: 46.250 lengthscales: 0.255, 0.246 noise: 0.106
Iter 44/100 - Loss: 47.110 lengthscales: 0.250, 0.241 noise: 0.101
Iter 45/100 - Loss: 45.541 lengthscales: 0.248, 0.237 noise: 0.096
Iter 46/100 - Loss: 41.711 lengthscales: 0.246, 0.237 noise: 0.091
Iter 47/100 - Loss: 40.852 lengthscales: 0.245, 0.237 noise: 0.086
Iter 48/100 - Loss: 39.588 lengthscales: 0.244, 0.239 noise: 0.082
Iter 49/100 - Loss: 36.817 lengthscales: 0.244, 0.241 noise: 0.078
Iter 50/100 - Loss: 34.773 lengthscales: 0.244, 0.244 noise: 0.074
Iter 51/100 - Loss: 31.050 lengthscales: 0.243, 0.247 noise: 0.070
Iter 52/100 - Loss: 28.448 lengthscales: 0.242, 0.248 noise: 0.067
Iter 53/100 - Loss: 29.796 lengthscales: 0.241, 0.246 noise: 0.063
Iter 54/100 - Loss: 25.501 lengthscales: 0.239, 0.243 noise: 0.060
Iter 55/100 - Loss: 28.542 lengthscales: 0.237, 0.238 noise: 0.057
Iter 56/100 - Loss: 23.089 lengthscales: 0.236, 0.231 noise: 0.054
Iter 57/100 - Loss: 19.792 lengthscales: 0.235, 0.225 noise: 0.051
Iter 58/100 - Loss: 20.285 lengthscales: 0.235, 0.219 noise: 0.049
Iter 59/100 - Loss: 16.047 lengthscales: 0.234, 0.214 noise: 0.046
Iter 60/100 - Loss: 15.160 lengthscales: 0.234, 0.211 noise: 0.044
Iter 61/100 - Loss: 13.038 lengthscales: 0.232, 0.209 noise: 0.042
Iter 62/100 - Loss: 13.928 lengthscales: 0.230, 0.209 noise: 0.040
Iter 63/100 - Loss: 9.312 lengthscales: 0.227, 0.210 noise: 0.038
Iter 64/100 - Loss: 7.950 lengthscales: 0.223, 0.212 noise: 0.036
Iter 65/100 - Loss: 3.461 lengthscales: 0.220, 0.215 noise: 0.034
Iter 66/100 - Loss: 5.609 lengthscales: 0.217, 0.217 noise: 0.033
Iter 67/100 - Loss: 2.204 lengthscales: 0.214, 0.218 noise: 0.031
Iter 68/100 - Loss: 0.597 lengthscales: 0.212, 0.219 noise: 0.029
Iter 69/100 - Loss: -1.111 lengthscales: 0.211, 0.217 noise: 0.028
Iter 70/100 - Loss: -2.389 lengthscales: 0.209, 0.214 noise: 0.027
Iter 71/100 - Loss: -3.256 lengthscales: 0.208, 0.210 noise: 0.025
Iter 72/100 - Loss: -4.180 lengthscales: 0.209, 0.207 noise: 0.024
Iter 73/100 - Loss: -6.345 lengthscales: 0.209, 0.205 noise: 0.023
Iter 74/100 - Loss: -10.216 lengthscales: 0.210, 0.204 noise: 0.022
Iter 75/100 - Loss: -11.749 lengthscales: 0.209, 0.204 noise: 0.021
Iter 76/100 - Loss: -10.651 lengthscales: 0.208, 0.204 noise: 0.020
Iter 77/100 - Loss: -12.092 lengthscales: 0.207, 0.205 noise: 0.019
Iter 78/100 - Loss: -14.908 lengthscales: 0.204, 0.206 noise: 0.018
Iter 79/100 - Loss: -16.482 lengthscales: 0.202, 0.208 noise: 0.017
Iter 80/100 - Loss: -17.962 lengthscales: 0.199, 0.207 noise: 0.016
Iter 81/100 - Loss: -23.044 lengthscales: 0.198, 0.207 noise: 0.016
Iter 82/100 - Loss: -20.867 lengthscales: 0.196, 0.205 noise: 0.015
Iter 83/100 - Loss: -20.908 lengthscales: 0.195, 0.203 noise: 0.014
Iter 84/100 - Loss: -25.210 lengthscales: 0.193, 0.201 noise: 0.013
Iter 85/100 - Loss: -24.521 lengthscales: 0.193, 0.199 noise: 0.013
Iter 86/100 - Loss: -25.571 lengthscales: 0.193, 0.199 noise: 0.012
Iter 87/100 - Loss: -26.477 lengthscales: 0.194, 0.199 noise: 0.012
Iter 88/100 - Loss: -26.940 lengthscales: 0.195, 0.200 noise: 0.011
Iter 89/100 - Loss: -27.446 lengthscales: 0.196, 0.199 noise: 0.011
Iter 90/100 - Loss: -30.484 lengthscales: 0.196, 0.198 noise: 0.010
Iter 91/100 - Loss: -29.450 lengthscales: 0.194, 0.196 noise: 0.010
Iter 92/100 - Loss: -28.761 lengthscales: 0.192, 0.198 noise: 0.009
Iter 93/100 - Loss: -34.818 lengthscales: 0.189, 0.200 noise: 0.009
Iter 94/100 - Loss: -39.531 lengthscales: 0.186, 0.203 noise: 0.009
Iter 95/100 - Loss: -38.291 lengthscales: 0.184, 0.202 noise: 0.008
Iter 96/100 - Loss: -38.961 lengthscales: 0.182, 0.200 noise: 0.008
Iter 97/100 - Loss: -41.103 lengthscales: 0.180, 0.197 noise: 0.007
Iter 98/100 - Loss: -42.563 lengthscales: 0.179, 0.194 noise: 0.007
Iter 99/100 - Loss: -42.571 lengthscales: 0.179, 0.191 noise: 0.007
Iter 100/100 - Loss: -37.692 lengthscales: 0.179, 0.191 noise: 0.007
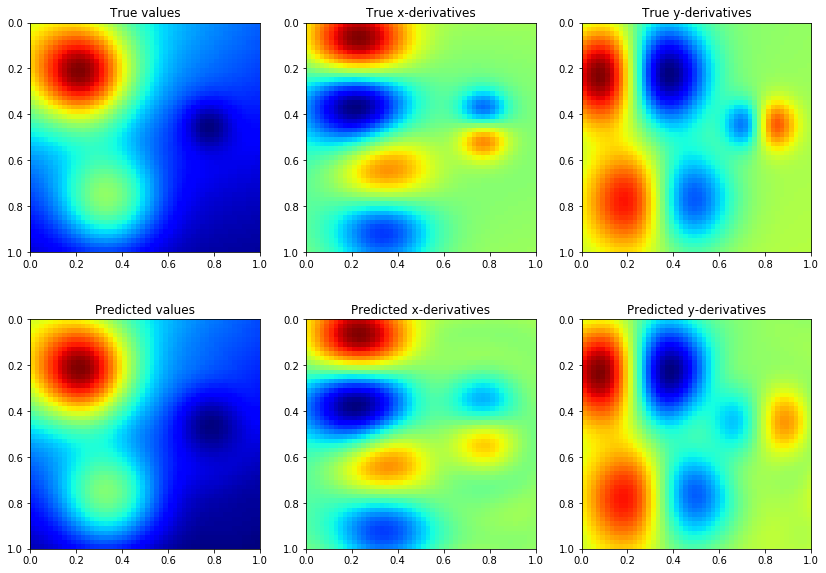
Model predictions are also similar to GP regression with only function values, but we need more CG iterations to get accurate estimates of the predictive variance
[6]:
# Set into eval mode
model.eval()
likelihood.eval()
# Initialize plots
fig, ax = plt.subplots(2, 3, figsize=(14, 10))
# Test points
n1, n2 = 50, 50
xv, yv = torch.meshgrid([torch.linspace(0, 1, n1), torch.linspace(0, 1, n2)])
f, dfx, dfy = franke(xv, yv)
# Make predictions
with torch.no_grad(), gpytorch.settings.fast_computations(log_prob=False, covar_root_decomposition=False):
test_x = torch.stack([xv.reshape(n1*n2, 1), yv.reshape(n1*n2, 1)], -1).squeeze(1)
predictions = likelihood(model(test_x))
mean = predictions.mean
extent = (xv.min(), xv.max(), yv.max(), yv.min())
ax[0, 0].imshow(f, extent=extent, cmap=cm.jet)
ax[0, 0].set_title('True values')
ax[0, 1].imshow(dfx, extent=extent, cmap=cm.jet)
ax[0, 1].set_title('True x-derivatives')
ax[0, 2].imshow(dfy, extent=extent, cmap=cm.jet)
ax[0, 2].set_title('True y-derivatives')
ax[1, 0].imshow(mean[:, 0].detach().numpy().reshape(n1, n2), extent=extent, cmap=cm.jet)
ax[1, 0].set_title('Predicted values')
ax[1, 1].imshow(mean[:, 1].detach().numpy().reshape(n1, n2), extent=extent, cmap=cm.jet)
ax[1, 1].set_title('Predicted x-derivatives')
ax[1, 2].imshow(mean[:, 2].detach().numpy().reshape(n1, n2), extent=extent, cmap=cm.jet)
ax[1, 2].set_title('Predicted y-derivatives')
None
[ ]: