[1]:
import tqdm
import math
import torch
import gpytorch
from matplotlib import pyplot as plt
# Make plots inline
%matplotlib inline
SVGP Model Updating¶
In this notebook, we will be describing a “fantasy model” strategy for stochastic variational GPs (SVGPs) analogous to fantasy modelling for exact GPs.
To understand what a “fantasy model” is, we first think about exact GPs. Imagine, we have trained a GP on some data \(\mathcal{D} := \{x_i, y_i\}_{i=1}^N\), which is the same as saying that \(\mathbf{y} \sim \mathcal{GP}(\mu(\mathbf{x}), K(\mathbf{x}, \mathbf{x}'))\).
If we observe some new data \(\mathcal{D}^*:= \{x_j, y_j\}_{j=1}^{N^*}\), then that data is easily incorporated into our GP model as \((\mathbf{y}, \mathbf{y}^*) \sim \mathcal{GP}(\mu([\mathbf{x}, \mathbf{x}^*]), K([\mathbf{x}, \mathbf{x}^*], [\mathbf{x}, \mathbf{x}^*]')\). To compute predictions with this new model (conditional on the same hyper-parameters), we could use the following piece of code for an exact GP:
updated_model = deepcopy(model)
updated_model.set_train_data(torch.cat((train_x, new_x)), torch.cat((train_y, new_y)), strict=False)
or we could take advantage of linear algebraic identies to efficiently produce the same model, which is the get_fantasy_model function for exact GPs in GPyTorch:
updated_model = model.get_fantasy_model(new_x, new_y)
The second approach is significantly more computationally efficient, costing \(\mathcal{O}((N^*)^2 N)\) time versus \(\mathcal{O}((N + N^*)^3)\) time.
In this tutorial notebook, we describe the online variational conditioning (OVC) approach of Maddox et al, ‘21 which provides a closed form method for updating SVGPs in the same manner as exact GPs are updated with respect ot new data, via the usage of the get_fantasy_model method.
Training Data¶
First, we construct some training data, here \(250\) data points from a noisy sine wave.
[2]:
train_x = torch.linspace(0, 3, 250).view(-1, 1).contiguous()
train_y = torch.sin(6. * train_x) + 0.3 * torch.randn_like(train_x)
plt.scatter(train_x, train_y, marker = "*", color = "black")
plt.xlabel("x")
plt.ylabel("y")
[2]:
Text(0, 0.5, 'y')

Model definition¶
Next, we define our model class definition. The only difference from a standard approximate GP is that we require the likelihood object to be a) Gaussian (for now) and b) to be stored inside of the ApproximateGP object.
[3]:
from gpytorch.models import ApproximateGP
from gpytorch.variational import CholeskyVariationalDistribution
from gpytorch.variational import VariationalStrategy
class GPModel(ApproximateGP):
def __init__(self, inducing_points, likelihood):
variational_distribution = CholeskyVariationalDistribution(inducing_points.size(0))
variational_strategy = VariationalStrategy(self, inducing_points, variational_distribution, learn_inducing_locations=True)
super(GPModel, self).__init__(variational_strategy)
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
self.likelihood = likelihood
def forward(self, x):
mean_x = self.mean_module(x)
covar_x = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)
We initialize the SVGP with \(25\) inducing points.
[4]:
likelihood = gpytorch.likelihoods.GaussianLikelihood()
model = GPModel(torch.randn(25, 1) + 2., likelihood)
Model Training¶
As we don’t have a lot of data, we train the model with full-batch (although this isn’t a restriction) and for \(500\) iterations (b/c our choice of inducing points may not have been very good).
[5]:
model.train()
likelihood.train()
optimizer = torch.optim.Adam([
{'params': model.parameters()},
# {'params': likelihood.parameters()},
], lr=0.1)
# Our loss object. We're using the VariationalELBO
mll = gpytorch.mlls.VariationalELBO(likelihood, model, num_data=train_y.size(0))
[6]:
iters = 500 + 1
for i in range(iters):
optimizer.zero_grad()
output = model(train_x)
loss = -mll(output, train_y.squeeze())
loss.backward()
optimizer.step()
if i % 50 == 0:
print("Iteration: ", i, "\t Loss:", loss.item())
Iteration: 0 Loss: 1.6754810810089111
Iteration: 50 Loss: 0.5079809427261353
Iteration: 100 Loss: 0.39197731018066406
Iteration: 150 Loss: 0.36815035343170166
Iteration: 200 Loss: 0.3656342625617981
Iteration: 250 Loss: 0.3653048574924469
Iteration: 300 Loss: 0.3654007315635681
Iteration: 350 Loss: 0.3680660128593445
Iteration: 400 Loss: 0.3646673262119293
Iteration: 450 Loss: 0.36463457345962524
Iteration: 500 Loss: 0.36551928520202637
Model Evaluation¶
Now, that we’ve trained our SVGP, we choose some data to evaluate it on – here \(250\) data points from \([0, 8]\) to illustrate the performance both for interpolation (on \([0,3]\)) and extrapolation (on \([3, 8]\)).
[7]:
model.eval()
likelihood.eval()
test_x = torch.linspace(0, 8, 250).view(-1,1)
with torch.no_grad():
posterior = likelihood(model(test_x))
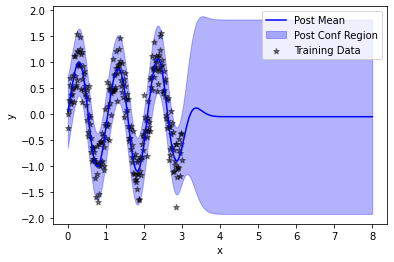
As expected, the posterior model fits the training data well but reverts to a zero mean and high prediction outside of the region of the training data.
[9]:
plt.plot(test_x, posterior.mean, color = "blue", label = "Post Mean")
plt.fill_between(test_x.squeeze(), *posterior.confidence_region(), color = "blue", alpha = 0.3, label = "Post Conf Region")
plt.scatter(train_x, train_y, color = "black", marker = "*", alpha = 0.5, label = "Training Data")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
[9]:
Text(0, 0.5, 'y')
Model Updating¶
Now, we choose \(25\) points to condition the model on – imagining that these data points have just been acquired, perhaps from an active learning or Bayesian optimization loop.
[10]:
val_x = torch.linspace(3, 5, 25).view(-1,1)
val_y = torch.sin(6. * val_x) + 0.3 * torch.randn_like(val_x)
[11]:
cond_model = model.variational_strategy.get_fantasy_model(inputs=val_x, targets=val_y.squeeze())
/Users/wesleymaddox/Documents/GitHub/wjm_gpytorch/gpytorch/utils/cholesky.py:40: NumericalWarning: A not p.d., added jitter of 1.0e-06 to the diagonal
warnings.warn(
/Users/wesleymaddox/Documents/GitHub/wjm_gpytorch/gpytorch/utils/cholesky.py:40: NumericalWarning: A not p.d., added jitter of 1.0e-05 to the diagonal
warnings.warn(
/Users/wesleymaddox/Documents/GitHub/wjm_gpytorch/gpytorch/utils/cholesky.py:40: NumericalWarning: A not p.d., added jitter of 1.0e-04 to the diagonal
warnings.warn(
Note that the updated model returned is an ExactGP class rather than a SVGP.
[12]:
cond_model
[12]:
_BaseExactGP(
(likelihood): GaussianLikelihood(
(noise_covar): HomoskedasticNoise(
(raw_noise_constraint): GreaterThan(1.000E-04)
)
)
(mean_module): ConstantMean()
(covar_module): ScaleKernel(
(base_kernel): RBFKernel(
(raw_lengthscale_constraint): Positive()
(distance_module): None
)
(raw_outputscale_constraint): Positive()
)
)
We compute its posterior distribution on the same testing dataset as before.
[13]:
with torch.no_grad():
updated_posterior = cond_model.likelihood(cond_model(test_x))
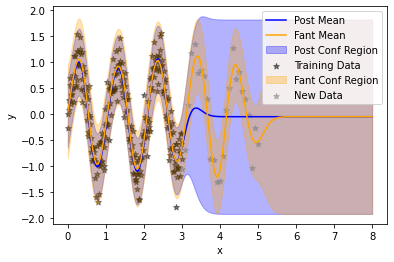
Finally, we plot the updated model, showing that the model has been updated to the newly observed data (grey) without forgetting the previous training data (black).
[15]:
plt.plot(test_x, posterior.mean, color = "blue", label = "Post Mean")
plt.fill_between(test_x.squeeze(), *posterior.confidence_region(), color = "blue", alpha = 0.3, label = "Post Conf Region")
plt.scatter(train_x, train_y, color = "black", marker = "*", alpha = 0.5, label = "Training Data")
plt.plot(test_x, updated_posterior.mean, color = "orange", label = "Fant Mean")
plt.fill_between(test_x.squeeze(), *updated_posterior.confidence_region(), color = "orange", alpha = 0.3, label = "Fant Conf Region")
plt.scatter(val_x, val_y, color = "grey", marker = "*", alpha = 0.5, label = "New Data")
plt.legend()
plt.xlabel("x")
plt.ylabel("y")
[15]:
Text(0, 0.5, 'y')
[ ]: