Latent Function Inference with Pyro + GPyTorch (Low-Level Interface)¶
Overview¶
In this example, we will give an overview of the low-level Pyro-GPyTorch integration. The low-level interface makes it possible to write GP models in a Pyro-style – i.e. defining your own model and guide functions.
These are the key differences between the high-level and low-level interface:
High level interface
Base class is
gpytorch.models.PyroGP.GPyTorch automatically defines the
modelandguidefunctions for Pyro.Best used when prediction is the primary goal
Low level interface
Base class is
gpytorch.models.ApproximateGP.User defines the
modelandguidefunctions for Pyro.Best used when inference is the primary goal
[1]:
import math
import torch
import pyro
import tqdm
import gpytorch
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
This example uses a GP to infer a latent function \(\lambda(x)\), which parameterises the exponential distribution:
where:
is a GP link function, which transforms the latent gaussian process variable:
In other words, given inputs \(X\) and observations \(Y\) drawn from exponential distribution with \(\lambda = \lambda(X)\), we want to find \(\lambda(X)\).
[2]:
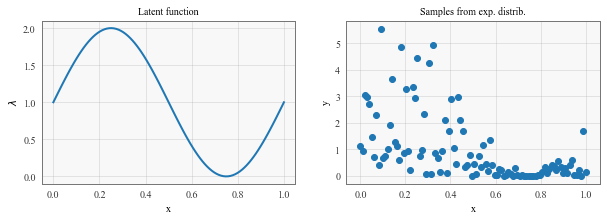
# Here we specify a 'true' latent function lambda
scale = lambda x: np.sin(2 * math.pi * x) + 1
# Generate synthetic data
# here we generate some synthetic samples
NSamp = 100
X = np.linspace(0, 1, 100)
fig, (lambdaf, samples) = plt.subplots(1, 2, figsize=(10, 3))
lambdaf.plot(X,scale(X))
lambdaf.set_xlabel('x')
lambdaf.set_ylabel('$\lambda$')
lambdaf.set_title('Latent function')
Y = np.zeros_like(X)
for i,x in enumerate(X):
Y[i] = np.random.exponential(scale(x), 1)
samples.scatter(X,Y)
samples.set_xlabel('x')
samples.set_ylabel('y')
samples.set_title('Samples from exp. distrib.')
[2]:
Text(0.5, 1.0, 'Samples from exp. distrib.')
[3]:
train_x = torch.tensor(X).float()
train_y = torch.tensor(Y).float()
Using the low-level Pyro/GPyTorch interface¶
The low-level iterface should look familiar if you’ve written Pyro models/guides before. We’ll use a gpytorch.models.ApproximateGP object to model the GP. To use the low-level interface, this object needs to define 3 functions:
forward(x)- which computes the prior GP mean and covariance at the supplied times.guide(x)- which defines the approximate GP posterior.model(x)- which does the following 3 thingsComputes the GP prior at
xConverts GP function samples into scale function samples, using the link function defined above.
Sample from the observed distribution
p(y | f). (This takes the place of a gpytorchLikelihoodthat we would’ve used in the high-level interface).
[4]:
class PVGPRegressionModel(gpytorch.models.ApproximateGP):
def __init__(self, num_inducing=64, name_prefix="mixture_gp"):
self.name_prefix = name_prefix
# Define all the variational stuff
inducing_points = torch.linspace(0, 1, num_inducing)
variational_strategy = gpytorch.variational.VariationalStrategy(
self, inducing_points,
gpytorch.variational.CholeskyVariationalDistribution(num_inducing_points=num_inducing)
)
# Standard initializtation
super().__init__(variational_strategy)
# Mean, covar, likelihood
self.mean_module = gpytorch.means.ConstantMean()
self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())
def forward(self, x):
mean = self.mean_module(x)
covar = self.covar_module(x)
return gpytorch.distributions.MultivariateNormal(mean, covar)
def guide(self, x, y):
# Get q(f) - variational (guide) distribution of latent function
function_dist = self.pyro_guide(x)
# Use a plate here to mark conditional independencies
with pyro.plate(self.name_prefix + ".data_plate", dim=-1):
# Sample from latent function distribution
pyro.sample(self.name_prefix + ".f(x)", function_dist)
def model(self, x, y):
pyro.module(self.name_prefix + ".gp", self)
# Get p(f) - prior distribution of latent function
function_dist = self.pyro_model(x)
# Use a plate here to mark conditional independencies
with pyro.plate(self.name_prefix + ".data_plate", dim=-1):
# Sample from latent function distribution
function_samples = pyro.sample(self.name_prefix + ".f(x)", function_dist)
# Use the link function to convert GP samples into scale samples
scale_samples = function_samples.exp()
# Sample from observed distribution
return pyro.sample(
self.name_prefix + ".y",
pyro.distributions.Exponential(scale_samples.reciprocal()), # rate = 1 / scale
obs=y
)
[5]:
model = PVGPRegressionModel()
Performing inference with Pyro¶
Unlike all the other examples in this library, PyroGP models use Pyro’s inference and optimization classes (rather than the classes provided by PyTorch).
If you are unfamiliar with Pyro’s inference tools, we recommend checking out the Pyro SVI tutorial.
[6]:
# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
num_iter = 2 if smoke_test else 200
num_particles = 1 if smoke_test else 256
def train():
optimizer = pyro.optim.Adam({"lr": 0.1})
elbo = pyro.infer.Trace_ELBO(num_particles=num_particles, vectorize_particles=True, retain_graph=True)
svi = pyro.infer.SVI(model.model, model.guide, optimizer, elbo)
model.train()
iterator = tqdm.notebook.tqdm(range(num_iter))
for i in iterator:
model.zero_grad()
loss = svi.step(train_x, train_y)
iterator.set_postfix(loss=loss, lengthscale=model.covar_module.base_kernel.lengthscale.item())
%time train()
CPU times: user 41.1 s, sys: 2.78 s, total: 43.9 s
Wall time: 6.54 s
In this example, we are only performing inference over the GP latent function (and its associated hyperparameters). In later examples, we will see that this basic loop also performs inference over any additional latent variables that we define.
Making predictions¶
For some problems, we simply want to use Pyro to perform inference over latent variables. However, we can also use the models’ (approximate) predictive posterior distribution. Making predictions with a PyroGP model is exactly the same as for standard GPyTorch models.
[7]:
# Here's a quick helper function for getting smoothed percentile values from samples
def percentiles_from_samples(samples, percentiles=[0.05, 0.5, 0.95]):
num_samples = samples.size(0)
samples = samples.sort(dim=0)[0]
# Get samples corresponding to percentile
percentile_samples = [samples[int(num_samples * percentile)] for percentile in percentiles]
# Smooth the samples
kernel = torch.full((1, 1, 5), fill_value=0.2)
percentiles_samples = [
torch.nn.functional.conv1d(percentile_sample.view(1, 1, -1), kernel, padding=2).view(-1)
for percentile_sample in percentile_samples
]
return percentile_samples
[8]:
# define test set (optionally on GPU)
denser = 2 # make test set 2 times denser then the training set
test_x = torch.linspace(0, 1, denser * NSamp).float()#.cuda()
model.eval()
with torch.no_grad():
output = model(test_x)
# Get E[exp(f)] via f_i ~ GP, 1/n \sum_{i=1}^{n} exp(f_i).
# Similarly get the 5th and 95th percentiles
samples = output(torch.Size([1000])).exp()
lower, mean, upper = percentiles_from_samples(samples)
# Draw some simulated y values
scale_sim = model(train_x)().exp()
y_sim = pyro.distributions.Exponential(scale_sim.reciprocal())()
[9]:
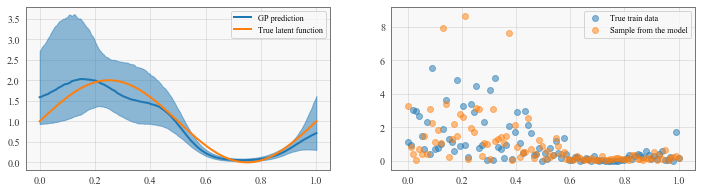
# visualize the result
fig, (func, samp) = plt.subplots(1, 2, figsize=(12, 3))
line, = func.plot(test_x, mean.detach().cpu().numpy(), label='GP prediction')
func.fill_between(
test_x, lower.detach().cpu().numpy(),
upper.detach().cpu().numpy(), color=line.get_color(), alpha=0.5
)
func.plot(test_x, scale(test_x), label='True latent function')
func.legend()
# sample from p(y|D,x) = \int p(y|f) p(f|D,x) df (doubly stochastic)
samp.scatter(train_x, train_y, alpha = 0.5, label='True train data')
samp.scatter(train_x, y_sim.cpu().detach().numpy(), alpha=0.5, label='Sample from the model')
samp.legend()
[9]:
<matplotlib.legend.Legend at 0x11e454fd0>
Next steps¶
This example probably could’ve also been done (slightly easier) using the high-level Pyro integration, or using GPyTorch’s native SVGP implementation. The low-level interface really comes in handy when a gpytorch Likelihood is difficult to define. For an example of this, see the next example which uses the low-level interface to infer the intensity function of a Cox process.