import math
import torch
import gpytorch
import matplotlib.pyplot as plt
%matplotlib inline

Different objective functions for Approximate GPs

(N.B. this tutorial assumes that you are familiar with inducing point methods. For an introduction to these methods, please see Quinonero-Candela and Rasmussen, 2005.)

Overview

Approximate Gaussian processes learn an approximate posterior distribution

\[p(\mathbf f(X) \mid y) \approx q(\mathbf f) = \int( p(\mathbf f \mid \mathbf u) \: q(\mathbf u) d \mathbf u\]

where \(\mathbf u\) are the function values at some inducing points \(\mathbf u\). Typically, \(q(\mathbf u)\) is chosen to be a multivariate Gaussian – i.e. \(q(\mathbf u) = \mathcal N (\mathbf m, \mathbf S)\).

We choose the approximate posterior \(\int( p(\mathbf f \mid \mathbf u) \: q(\mathbf u) d \mathbf u\) by optimizing the parameters of \(q(\mathbf u)\) (i.e. \(\mathbf m\) and \(\mathbf S\). There are several objectives that we can use for optimization. We’ll test out the following two:

1. The Variational ELBO (see Hensman et al., 2015)

2. The Predictive Log Likelihood (see Jankowiak et al., 2020).

Experimental setup

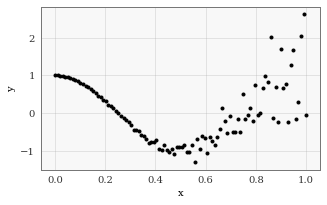
We’re going to train an approximate GP on a 1D regression dataset with heteroskedastic noise.

# Define some training data
train_x = torch.linspace(0, 1, 100)
train_y = torch.cos(train_x * 2 * math.pi) + torch.randn(100).mul(train_x.pow(3) * 1.)

fig, ax = plt.subplots(1, 1, figsize=(5, 3))
ax.scatter(train_x, train_y, c='k', marker='.', label="Data")
ax.set(xlabel="x", ylabel="y")

[Text(0, 0.5, 'y'), Text(0.5, 0, 'x')]

Here’s a simple approximate GP model, and a script to optimize/test the model with different objective functions:

class ApproximateGPModel(gpytorch.models.ApproximateGP):
    def __init__(self, inducing_points):
        variational_distribution = gpytorch.variational.CholeskyVariationalDistribution(inducing_points.size(-1))
        variational_strategy = gpytorch.variational.VariationalStrategy(
            self, inducing_points, variational_distribution, learn_inducing_locations=True
        )
        super().__init__(variational_strategy)
        self.mean_module = gpytorch.means.ConstantMean()
        self.covar_module = gpytorch.kernels.ScaleKernel(gpytorch.kernels.RBFKernel())

    def forward(self, x):
        mean_x = self.mean_module(x)
        covar_x = self.covar_module(x)
        return gpytorch.distributions.MultivariateNormal(mean_x, covar_x)

# this is for running the notebook in our testing framework
import os
smoke_test = ('CI' in os.environ)
training_iterations = 2 if smoke_test else 50


# Our testing script takes in a GPyTorch MLL (objective function) class
# and then trains/tests an approximate GP with it on the supplied dataset

def train_and_test_approximate_gp(objective_function_cls):
    model = ApproximateGPModel(torch.linspace(0, 1, 100))
    likelihood = gpytorch.likelihoods.GaussianLikelihood()
    objective_function = objective_function_cls(likelihood, model, num_data=train_y.numel())
    optimizer = torch.optim.Adam(list(model.parameters()) + list(likelihood.parameters()), lr=0.1)

    # Train
    model.train()
    likelihood.train()
    for _ in range(training_iterations):
        output = model(train_x)
        loss = -objective_function(output, train_y)
        loss.backward()
        optimizer.step()
        optimizer.zero_grad()

    # Test
    model.eval()
    likelihood.eval()
    with torch.no_grad():
        f_dist = model(train_x)
        mean = f_dist.mean
        f_lower, f_upper = f_dist.confidence_region()
        y_dist = likelihood(f_dist)
        y_lower, y_upper = y_dist.confidence_region()

    # Plot model
    fig, ax = plt.subplots(1, 1, figsize=(5, 3))
    line, = ax.plot(train_x, mean, "blue")
    ax.fill_between(train_x, f_lower, f_upper, color=line.get_color(), alpha=0.3, label="q(f)")
    ax.fill_between(train_x, y_lower, y_upper, color=line.get_color(), alpha=0.1, label="p(y)")
    ax.scatter(train_x, train_y, c='k', marker='.', label="Data")
    ax.legend(loc="best")
    ax.set(xlabel="x", ylabel="y")

Objective Funtion 1) The Variational ELBO

The variational evidence lower bound - or ELBO - is the most common objective function. It can be derived as an lower bound on the likelihood \(p(\mathbf y \! \mid \! \mathbf X)\):

\[\mathcal{L}_\text{ELBO} = \sum_{i=1}^N \mathbb{E}_{q( \mathbf u)} \left[ \mathbb{E}_{f( \mathbf f \mid \mathbf u)} \left[ \log p( y_i \! \mid \! f_i) \right] \right] - \beta \: \text{KL} \left[ q( \mathbf u) \Vert p( \mathbf u) \right]\]

where \(N\) is the number of datapoints and \(p(\mathbf u)\) is the prior distribution for the inducing function values. For more information on this derivation, see Hensman et al., 2015.

How to use the variational ELBO in GPyTorch

In GPyTorch, this objective function is available as gpytorch.mlls.VariationalELBO.

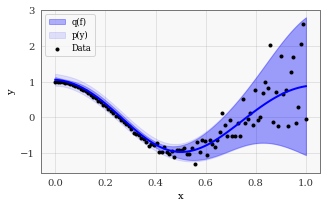
train_and_test_approximate_gp(gpytorch.mlls.VariationalELBO)

Objective Funtion 2) The Predictive Log Likelihood

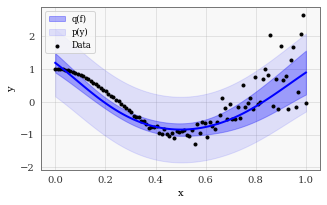
The predictive log likelihood is an alternative to the variational ELBO that was proposed in Jankowiak et al., 2020. It typically produces predictive variances than the gpytorch.mlls.VariationalELBO objective.

\[\begin{split}\begin{align} \mathcal{L}_\text{PLL} &= \mathbb{E}_{p_\text{data}( y, \mathbf x )} \left[ \log p( y \! \mid \! \mathbf x) \right] - \beta \: \text{KL} \left[ q( \mathbf u) \Vert p( \mathbf u) \right] \\ &\approx \sum_{i=1}^N \log \mathbb{E}_{q(\mathbf u)} \left[ \int p( y_i \! \mid \! f_i) p(f_i \! \mid \! \mathbf u) \: d f_i \right] - \beta \: \text{KL} \left[ q( \mathbf u) \Vert p( \mathbf u) \right] \end{align}\end{split}\]

Note that this objective is very similar to the variational ELBO. The only difference is that the \(\log\) occurs outside the expectation \(\mathbb E_{q(\mathbf u)}\). This difference results in very different predictive performance.

How to use the predictive log likelihood in GPyTorch

In GPyTorch, this objective function is available as gpytorch.mlls.PredictiveLogLikelihood.

train_and_test_approximate_gp(gpytorch.mlls.PredictiveLogLikelihood)